Just post

pemandangan circuit

http://www.math.ucdavis.edu/~daddel/linear_algebra_appl/Applications/Electrical_Circuits/Electrical_Circuits.html

syawal dan iza

Introduction

CIRCUITS

HOW  CAN YOU GET CHARGES TO FLOW ??

“PUMPING” CHARGES

·         To make Charge carriers flow through  a resistor 

·         Need to establish a potential difference between the ends device

·         Connect each end of the resistor to one plate of charged capacitor

But..

·         The flow of charge acts to discharge the capacitor

·         Bringing the plates to the same potential

·         No longer an electric field in resistor so the flow of charges stop

We need a “Charge pump” To produce a steady flow of charge

·         Charge pump –device that doing work on charge carriers so that the potential differences between a pair of terminals are maintains ---

This device called as emf device(electromotive force)

·         The motion of charge carriers in terms of the required energy(the emf devices supplies the energy for the motion via the work it does.

·         Common emf ----battery,electric generator,solar cells,fuel cells,thermopiles

                       ----electric eels..

                       ------they do the work on charge carriers

                       ------maintain a potential difference between their terminals

WORK , ENERGY , EMF

Simple circuit:

--- Consider emf as the battery.. ( positive terminal --- higher elecrtric potential than                          negative terminal)

--- if emf not connected to a circuit ,internal chemistry of the device does not cause any net flow of charges within it)

--- within emf , +ve charge carriers move from region negative terminal àpositive terminal)

--- but the electric field between the terminals is opposite from this motion (positive terminal à negative terminal)

--- there must be some source of energy within device enabling it to do work on the charges forcing them to move.(maybe chemical in battery or mechanical forces in electric generator)

View of work and energy transfer

--- definition emf :

in words:work per unit charge

                                  :moving charge from its low-potential terminal to its high

                                   Potential terminal ( -ve to +ve )  --- unit volt.

Ideal emf : lacks any internal resistance to the internal movement of charge  from terminal to terminal.

                 :potential difference between terminal = emf

Real emf : has internal resistance to the internal movement of charge.

                :when connected to the circuit

                -if there is no current through it , potential difference = emf

                -if there is current through it , potential difference not same with emf

              

Circuit containing :

--- two ideal rechargeable batteries A and B

--- resistance R

--- electric motor M

Process occur :

1)   Batteries are connected to send charges around the circuit in opposite direction

2)   Actual direction of current determined from battery with larger emf (B)

3)   Chemical energy in Battery B decreasing because  energy  transferred to the charge carriers passing through it

4)   Chemical energy in Battery A  increasing because current in it is directed from positive terminal to negative terminal.

5)   Battery B charges battery A , providing energy to motor M and energy dissipated by resistance R

                                                                                                                                                  

 Fazihan

Multi-loop Circuits and Kirchoff's Rules

Before talking about what a multi-loop circuit is, it is helpful to define two terms, junction and branch.
A junction is a point where at least three circuit paths meet.
A branch is a path connecting two junctions.
In the circuit below, there are two junctions, labeled a and b. There are three branches: these are the three paths from a to b.

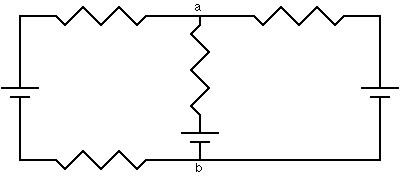
Multi-loop circuits

In a circuit involving one battery and a number of resistors in series and/or parallel, the resistors can generally be reduced to a single equivalent resistor. With more than one battery, the situation is trickier. If all the batteries are part of one branch they can be combined into a single equivalent battery. Generally, the batteries will be part of different branches, and another method has to be used to analyze the circuit to find the current in each branch. Circuits like this are known as multi-loop circuits.
Finding the current in all branches of a multi-loop circuit (or the emf of a battery or the value of a resistor) is done by following guidelines known as Kirchoff's rules. These guidelines also apply to very simple circuits.
Kirchoff's first rule : the junction rule. The sum of the currents coming in to a junction is equal to the sum leaving the junction. (Basically this is conservation of charge)
Kirchoff's second rule : the loop rule. The sum of all the potential differences around a complete loop is equal to zero. (Conservation of energy)
There are two different methods for analyzing circuits. The standard method in physics, which is the one followed by the textbook, is the branch current method. There is another method, the loop current method, but we won't worry about that one.

The branch current method

To analyze a circuit using the branch-current method involves three steps:

1. Label the current and the current direction in each branch. Sometimes it's hard to tell which is the correct direction for the current in a particular loop. That does NOT matter. Simply pick a direction. If you guess wrong, you¹ll get a negative value. The value is correct, and the negative sign means that the current direction is opposite to the way you guessed. You should use the negative sign in your calculations, however.
2. Use Kirchoff's first rule to write down current equations for each junction that gives you a different equation. For a circuit with two inner loops and two junctions, one current equation is enough because both junctions give you the same equation.
3. Use Kirchoff's second rule to write down loop equations for as many loops as it takes to include each branch at least once. To write down a loop equation, you choose a starting point, and then walk around the loop in one direction until you get back to the starting point. As you cross batteries and resistors, write down each voltage change. Add these voltage gains and losses up and set them equal to zero.

When you cross a battery from the - side to the + side, that's a positive change. Going the other way gives you a drop in potential, so that's a negative change.
When you cross a resistor in the same direction as the current, that's also a drop in potential so it's a negative change in potential. Crossing a resistor in the opposite direction as the current gives you a positive change in potential.

An example

Running through an example should help clarify how Kirchoff's rules are used. Consider the circuit below:


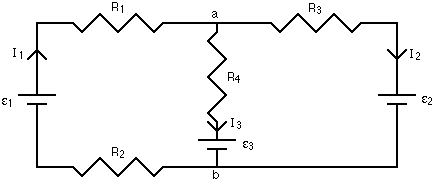
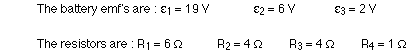
Step 1 of the branch current method has already been done. The currents have been labeled in each branch of the circuit, and the directions are shown with arrows. Again, you don't have to be sure of these directions at this point. Simply choose directions, and if any of the currents come out to have negative signs, all it means is that the direction of that current is opposite to the way you've shown on your diagram.
Applying step 2 of the branch current method means looking at the junctions, and writing down a current equation. At junction a, the total current coming in to the junction equals the total current flowing away. This gives:
at junction a : I₁ = I₂ + I₃
If we applied the junction rule at junction b, we'd get the same equation. So, applying the junction rule at one of the junctions is all we need to do. In some cases you will need to get equations from more than one junction, but you'll never need to get an equation for every junction.
There are three unknowns, the three currents, so we need to have three equations. One came from the junction rule; the other two come from going to step 3 and applying the loop rule. There are three loops to use in this circuit: the inside loop on the left, the inside loop on the right, and the loop that goes all the way around the outside. We just need to write down loop equations until each branch has been used at least once, though, so using any two of the three loops in this case is sufficient.
When applying the loop equation, the first step is to choose a starting point on one loop. Then walk around the loop, in either direction, and write down the change in potential when you go through a battery or resistor. When the potential increases, the change is positive; when the potential decreases, the change is negative. When you get back to your starting point, add up all the potential changes and set this sum equal to zero, because the net change should be zero when you get back to where you started.
When you pass through a battery from minus to plus, that's a positive change in potential, equal to the emf of the battery. If you go through from plus to minus, the change in potential is equal to minus the emf of the battery.
Current flows from high to low potential through a resistor. If you pass through a resistor in the same direction as the current, the potential, given by IR, will decrease, so it will have a minus sign. If you go through a resistor opposite to the direction of the current, you're going from lower to higher potential, and the IR change in potential has a plus sign.
Keeping all this in mind, let's write down the loop equation for the inside loop on the left side. Picking a starting point as the bottom left corner, and moving clockwise around the loop gives:

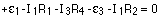
Make sure you match the current to the resistor; there is one current for each branch, and a loop has at least two branches in it.
The inner loop on the right side can be used to get the second loop equation. Starting in the bottom right corner and going counter-clockwise gives:

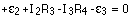
Plugging in the values for the resistances and battery emf's gives, for the three equations:

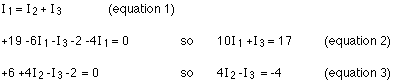
The simplest way to solve this is to look at which variable shows up in both loop equations (equations 2 and 3), solve for that variable in equation 1, and substitute it in in equations 2 and 3.
Rearranging equation 1 gives:

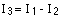
Substituting this into equation 2 gives:

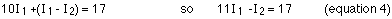
Making the same substitution into equation 3 gives:

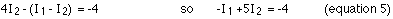
This set of two equations in two unknowns can be reduced to one equation in one unknown by multiplying equation 4 by 5 (the number 5, not equation 5!) and adding the result to equation 5.

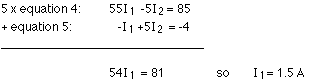
Substituting this into equation 5 gives:
I₂ = ( -4 + 1.5 ) / 5 = -0.5 A
The negative sign means that the current is 0.5 A in the direction opposite to that shown on the diagram. Solving for the current in the middle branch from equation 1 gives:
I₃ = 1.5 - (-0.5) = 2.0 A
An excellent way to check your answer is to go back and label the voltage at each point in the circuit. If everything is consistent, your answer is fine. To label the voltage, the simplest thing to do is choose one point to be zero volts. It's just the difference in potential between points that matters, so you can define one point to be whatever potential you think is convenient, and use that as your reference point. My habit is to set the negative side of one of the batteries to zero volts, and measure everything else with respect to that.

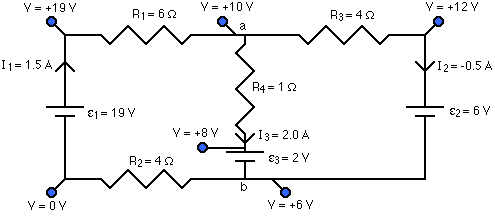
In this example circuit, when the potential at all the points is labeled, everything is consistent. What this means is that when you go from junction b to junction a by any route, and figure out what the potential at a is, you get the same answer for each route. If you got different answers, that would be a big hint that you did something wrong in solving for the currents. Note also that you have to account for any of the currents coming out to be negative, and going the opposite way from what you had originally drawn.
One final note: you can use this method of circuit analysis to solve for more things than just the current. If one or more of the currents was known (maybe the circuit has an ammeter or two, measuring the current magnitude and direction in one or two branches) then an unknown battery emf or an unknown resistance could be found instead.

Meters

It is often useful to measure the voltage or current in a circuit. A voltmeter is a device used to measure voltage, while a meter measuring current is an ammeter. Meters are either analog or digital devices. Analog meters show the output on a scale with a needle, while digital devices produce a digital readout. Analog voltmeters and ammeters are both based on a device called a galvanometer. Because this is a magnetic device, we'll come back to that in the next chapter. Digital voltmeters and ammeters generally rely on measuring the voltage across a known resistor, and converting that voltage to a digital value for display.

Voltmeters

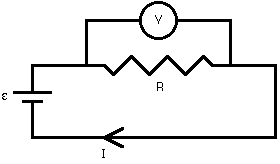
Resistors in parallel have the same voltage across them, so if you want to measure the voltage across a circuit element like a resistor, you place the voltmeter in parallel with the resistor. The voltmeter is shown in the circuit diagram as a V in a circle, and it acts as another resistor. To prevent the voltmeter from changing the current in the circuit (and therefore the voltage across the resistor), the voltmeter must have a resistance much larger than the resistor's. With a large voltmeter resistance, hardly any of the current in the circuit makes a detour through the meter.

Ammeters

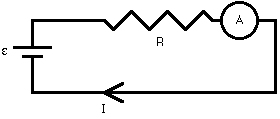
Remember that resistors in series have the same current flowing through them. An ammeter, then, must be placed in series with a resistor to measure the current through the resistor. On a circuit diagram, an ammeter is shown as an A in a circle. Again, the ammeter acts as a resistor, so to minimize its impact on the circuit it must have a small resistance relative to the resistance of the resitor whose current is being measured.

RC Circuits

Resistors are relatively simple circuit elements. When a resistor or a set of resistors is connected to a voltage source, the current is constant. If a capacitor is added to the circuit, the situation changes. In a simple series circuit, with a battery, resistor, and capacitor in series, the current will follow an exponential decay. The time it takes to decay is determined by the resistance (R) and capacitance (C) in the circuit.

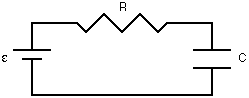
A capacitor is a device for storing charge. In some sense, a capacitor acts like a temporary battery. When a capacitor is connected through a resistor to a battery, charge from the battery is stored in the capacitor. This causes a potential difference to build up across the capacitor, which opposes the potential difference of the battery. As this potential difference builds, the current in the circuit decreases.
If the capacitor is connected to a battery with a voltage of Vo, the voltage across the capacitor varies with time according to the equation:

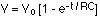
The current in the circuit varies with time according to the equation:

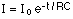
Graphs of voltage and current as a function of time while the capacitor charges are shown below.

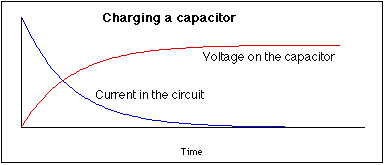
The product of the resistance and capacitance, RC, in the circuit is known as the time constant. This is a measure of how fast the capacitor will charge or discharge.
After charging a capacitor with a battery, the battery can be removed and the capacitor can be used to supply current to the circuit. In this case, the current obeys the same equation as above, decaying away exponentially, and the voltage across the capacitor will vary as:

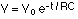
Graphs of the voltage and current while the capacitor discharges are shown here. The current is shown negative because it is opposite in direction to the current when the capacitor charges.

Currents in nerve cells

In the human body, signals are sent back and forth between muscles and the brain, as well as from our sensory receptors (eyes, ears, touch sensors, etc.) to the brain, along nerve cells. These nerve impulses are electrical signals that are transmitted along the body, or axon, of a nerve cell.
The axon is simply a long tube built to carry electrical signals. A potential difference of about 70 mV exists across the cell membrane when the cell is in its resting state; this is due to a small imbalance in the concentration of ions inside and outside the cell. The ions primarily responsible for the propagation of a nerve impulse are potassium (K⁺) and sodium +.
The potential inside the cell is at -70 mV with respect to the outside. Consider one point on the axon. If the potential inside the axon at that point is raised by a small amount, nothing much happens. If the potential inside is raised to about -55 mV, however, the permeability of the cell membrane changes. This causes sodium ions to enter the cell, raising the potential inside to about +50 mV. At this point the membrane becomes impermeable to sodium again, and potassium ions flow out of the cell, restoring the axon at that point to its rest state.
That brief rise to +50 mV at point A on the axon, however, causes the potential to rise at point B, leading to an ion transfer there, causing the potential there to shoot up to +50 mV, thereby affecting the potential at point C, etc. This is how nerve impulses are transmitted along the nerve cell.

©cahayasyawal

Video for Simple Circuit

Today, I would like to post two videos that related to circuit. Note that the video with the longer duration(the upper one) is part 1 for the circuit. Hope you enjoy this video and gain some knowledge regarding this topic.  :)

                                                       written by : Quraisya

Time Constant

Assalamualaikum.

In this post, I would like to tell you about TIME CONSTANT.

The Time Constant

• All Electrical or Electronic circuits or systems suffer from some form of "time-delay" between its input and output, when a signal or voltage, either continuous, ( DC ) or alternating ( AC ) is firstly applied to it. 

• This delay is generally known as the time delay or Time Constant of the circuit and it is the time response of the circuit when a step voltage or signal is firstly applied. The resultant time constant of any circuit or system will mainly depend upon the reactive components either capacitive or inductive connected to it and is a measurement of the response time with units of, Tau - τ

• When an increasing DC voltage is applied to a discharged Capacitor the capacitor draws a charging current and "charges up", and when the voltage is reduced, the capacitor discharges in the opposite direction. Because capacitors are able to store electrical energy they act like small batteries and can store or release the energy as required.

• The charge on the plates of the capacitor is given as: Q = CV. This charging (storage) and discharging (release) of a capacitors energy is never instant but takes a certain amount of time to occur with the time taken for the capacitor to charge or discharge to within a certain percentage of its maximum supply value being known as its Time Constant ( τ ).

• So mathematically we can say that the time required for a capacitor to charge up to one time constant is given as:
  
  Where, R is in Ω's and C in Farads.
  
  
  
  
  Now, I will show you an example that I obtain from internet. It is just a simple example for your further understanding. 
  
  
  
  
  
  
  
  
  
  

  Calculate the time constant of the following circuit.
  	The time constant τ is found using the formula T = R x C in seconds. Therefore the time constant τ is: T = R x C = 47k x 1000uF = 47 Secs
  a) What value will be the voltage across the capacitor at 0.7 time constants?
  At 0.7 time constants ( 0.7T ) Vc = 0.5Vs. Therefore, Vc = 0.5 x 5V = 2.5V
  b) What value will be the voltage across the capacitor at 1 time constant?
  At 1 time constant ( 1T ) Vc = 0.63Vs. Therefore, Vc = 0.63 x 5V = 3.15V
  c) How long will it take to "fully charge" the capacitor?
  The capacitor will be fully charged at 5 time constants.         1 time constant ( 1T ) = 47 seconds, (from above). Therefore, 5T = 5 x 47 = 235 secs That's all from me. Before I end up my post, I would like to share a few quotes to all of my comrades.

  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
                                                                                            Written by : Quraisya

Ammeter vs Voltmeter

The Difference Between Ammeter and Voltmeter

Assalamualaikum. Hai guys, how are you today? :)  I hope you enjoy living in the presence, " Enjoy each day or the moment you are in because once it's gone it's gone" . Let's live to the fullest my comrades. 

So, all of you already know what the topic that I want to write about.    erk... WHAT? YOU DON'T KNOW?  It is IMPOSSIBLE... It is written clearly above, hehhehe. Sorry, I'm just joking, out of the blue.

Ok, let us start seriously. Electricity, just like any other physical characteristic, can be quantified; although it is a bit more difficult. The two main characteristics of electricity are voltage and current and to measure them both, we have the voltmeter and ammeter. The voltmeter measure the voltage between two points while the ammeter measure the current through it.

First, let us take a look to the difference in functionality. The obvious difference between a voltmeter and ammeter is that the former is used to make an accurate measurement of potential difference, while the latter is used to measure current flowing between two points. They differ in functionality but they measure two aspects of an electrical measurement which are voltage and amperage. Nowadays, multi meter instruments are available that do the job of a voltmeter and an ammeter.

There is a difference between how a voltmeter and an ammeter are connected in a circuit. When measuring the voltage across a resistor or a conductor element, the voltmeter is always connected in parallel. As opposed to this, to measure the current flowing through a circuit element an ammeter should be connected in series.

Summary:

1. An ammeter measures current while a voltmeter measure voltage
2. An ammeter is to be connected in series while a voltmeter is connected in parallel
3. An ammeter needs to approximate a short-circuit while a voltmeter needs to approximate an open circuit
4. Contactless ammeters are available while

Read more at Buzzle: http://www.buzzle.com/articles/voltmeter-vs-ammeter.html

Read more: Difference Between Ammeter and Voltmeter | Difference Between | Ammeter vs Voltmeter http://www.differencebetween.net/science/difference-between-ammeter-and-voltmeter/#ixzz2FBB5YQr8

Before I end up my post here, I would like to post a quotes from one of the famous Physicist, Albert Einstein that can buck you up when you are depressed. 

                                                                                                                      Written by : Quraisya

RC Circuit, Charging and Discharging Capacitor

Assalamualaikum.

Hai guys~! We meet again in this blog with the permission of our Greatest and Merciful LORD, ALLAH. Say Alhamdulillah, Thank You Allah for the opportunities given, opportunity to breath, opportunity to learn, opportunity to read this post, and many more.

In this post, we will talk about RC CIRCUITS. What is RC Circuit actually?

RC Circuits

An RC circuit is a circuit with both a resistor (R) and a capacitor (C). RC circuits are freqent element in electronic devices. They also play an important role in the transmission of electrical signals in nerve cells.

A capacitor can store energy and a resistor placed in series with it will control the rate at which it charges or discharges. This produces a characteristic time dependence that turns out to be exponential. The crucial parameter that describes the time dependence is the "time constant" R C .


We will confine our studies to the following circuit, in which the switch can be moved between positions a and b.

Let us begin by reviewing some facts about capacitors:

1. The charge on a capacitor cannot change instantaneously. The current is given by I = DQ / Dt. Hence the change in charge DQ = I Dt goes to zero as the time interval Dt goes to zero.
2. The current flowing into a capacitor in the steady state that is reached after a long time interval is zero. Since charge builds up on a capacitor rather than flowing through it, charge can build up until the point that the voltage V=Q/C balances out the external voltage pushing charge onto the capacitor.

When a capacitor of capacitance C is in series with a battery of voltage V_b and a resistor of resistance R, the voltage drops must be:

,

which is a statement that the voltage gained going across the battery must equal the voltage drop across the capacitor plus the voltage drop across the resistor. An equation where the rate of change of a quantitity (DQ/Dt) is proportional to the quantity (DQ) will always have an exponential solution. We consider two instances:

1. Discharging the capacitor: The capacitor initially is connected (switch in position a) for a long time, and is then disconnected by moving the switch to b at time t = 0. The capacitor then discharges, leaving the capacitor without charge or voltage after a long time.
   
   
2. Charging the capacitor: The switch is in position b for a long time, allowing the capacitor to have no charge. At time t = 0, the switch is changed to a and the capacitor charges.
   
   

	Discharging	Charging
Charge
Current
Voltage

For a better understanding, you can dowload the following PDF :

• http://groups.physics.northwestern.edu/lab/DOWNLOAD/rc_circ.pdf

Or you can view or download the PPT that I have attached :

• https://www.google.com.my/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&ved=0CDIQFjAA&url=http%3A%2F%2Fhighered.mcgraw-hill.com%2Fsites%2Fdl%2Ffree%2F007301267x%2F294297%2FChapter32B.ppt&ei=wonNUIX-E4bwrQeYtoCoDg&usg=AFQjCNGqSZqWPXSaq8d9oy_WxpCTAc9L1g&sig2=kRcydjfzp23HSa0su01SCg

       References : http://en.wikipedia.org/wiki/RC_circuit

                                                                                         Written by : Quraisya